Have you ever thought about symmetry; how symmetric are objects such as cubes, snowflakes, or even mathematic objects, and how are those symmetries defined? Mathematicians have too and developed an entire field to study symmetry called group theory. Group theory has been studied for nearly two-hundred years and continues to reveal the rather strange quirks of math. Before further discussion, the terms group, set, and symmetry need to be defined.

Definitions

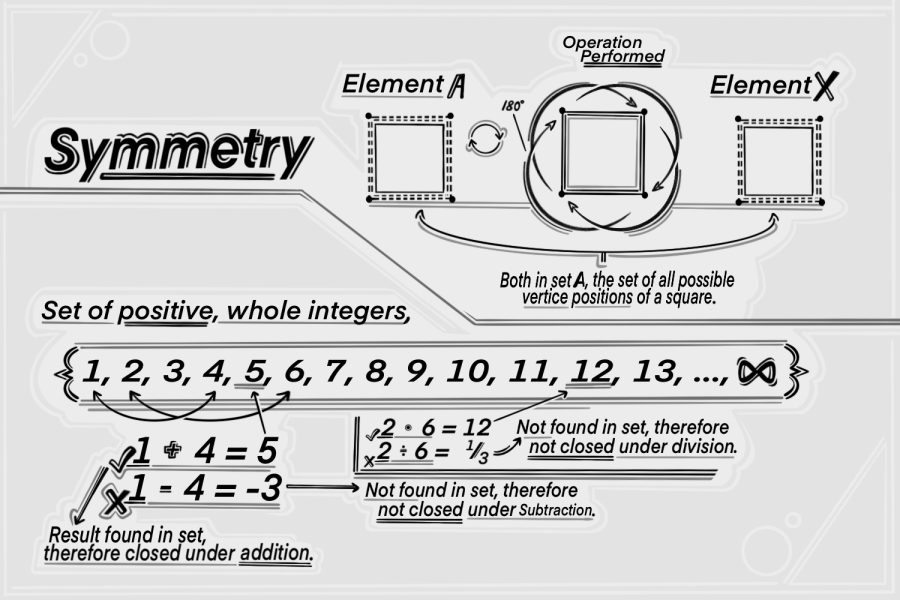
Groups are mathematical objects, not physical objects but merely abstract things, that describe all possible symmetries within a set. Sets are collections of things, typically related. Any collection of things can constitute a set. For example, all the items within a bag can be a set, all the trees on Earth can be a set, the faces and vertices on a cube can be a set, the entire number line can be a set, etc. Symmetry can be defined as the ability to perform an action on a set such that the result could be an element (item) in the set. This is also known as closure.

Examples

If the possible positions of the vertices of a square make a set (via rotation or reflection/flipping), then rotating the vertices clockwise 180 degrees would result in another square whose vertices would be found in the same set of the possible positions of vertices. You could say, “the set of the positions of a square’s vertices is closed under rotation.” That means the square’s vertices are symmetric when you apply the operation (the action you perform on a set) of rotation. The operation must also be binary; an action performed on two elements of a set to result in a third element. Another example is the closure of the set of all positive whole numbers under addition and multiplication. Any positive whole number added to or multiplied by another will result in another positive whole number found in the same positive whole number set. This set is not closed under division or subtraction because division may result in non-whole numbers (decimals and/or irrational numbers) and subtraction may result in negative numbers. Neither types of these numbers are in the set of positive whole numbers. A group, say group A, is the combination of binary operations and the set on which those operations are performed.

This was a simple, well not really, introduction to group theory. To learn more, watch 3Blue1Brown’s video on groups which dives deeper into the topic.